exchangeability

Formalization of exchangeability and de Finetti's theorem in Lean 4.

Overview

This project formalizes the de Finetti-Ryll-Nardzewski theorem (Kallenberg's Theorem 1.1), which establishes a three-way equivalence for infinite sequences on standard Borel spaces:

(i) Contractable ⟺ (ii) Exchangeable ⟺ (iii) Conditionally i.i.d.

We implement all three proofs from Kallenberg (2005) of the key implication contractable → conditionally i.i.d.:

Martingale Approach (Default)
- Kallenberg's "third proof" (after Aldous)
- Elegant probabilistic argument using reverse martingales
- Exchangeability/DeFinetti/ViaMartingale/ (13 files)
L² Approach
- Kallenberg's "second proof" - Elementary L² contractability bounds
- Lightest dependencies (no ergodic theory required)
- Formalized for ℝ-valued sequences with L² integrability
- Exchangeability/DeFinetti/ViaL2/ (12 files)
Koopman Approach
- Kallenberg's "first proof" - Mean Ergodic Theorem
- Deep connection to dynamical systems and ergodic theory
- Exchangeability/DeFinetti/ViaKoopman/ (18 files)

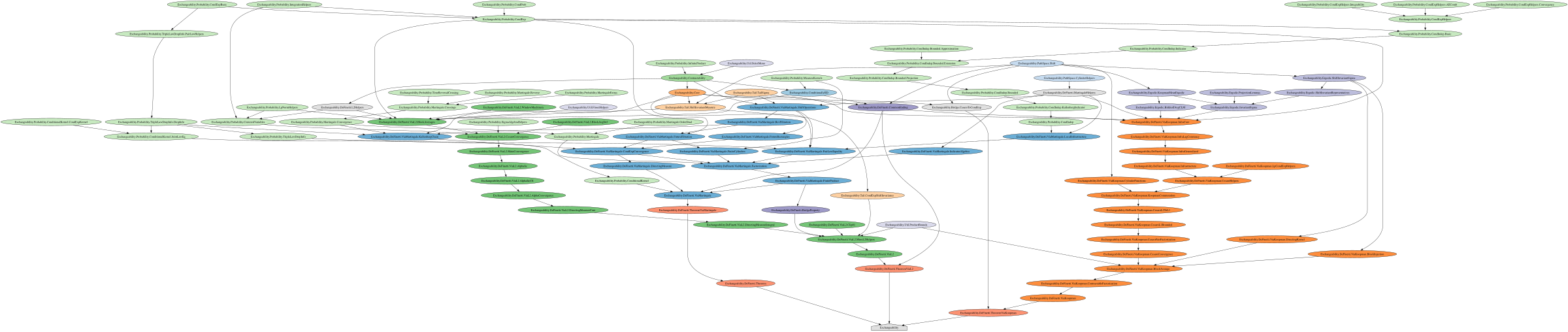
Import Graph

Modules colored by proof: 🔵 Martingale 🟢 L² 🟠 Koopman
Interactive · All declarations · Blueprint only

Quick Start

Prerequisites

Lean 4 (this project uses lean-toolchain pinned to 4.27.0-rc1)
elan (Lean version manager)

Installation

# Install elan
curl -sSf https://raw.githubusercontent.com/leanprover/elan/master/elan-init.sh | sh

# Clone and build
git clone https://github.com/cameronfreer/exchangeability.git
cd exchangeability
lake build

Using the Library

import Exchangeability

-- de Finetti's theorem (uses martingale proof by default)
example {Ω : Type*} [MeasurableSpace Ω] [StandardBorelSpace Ω]
    {α : Type*} [MeasurableSpace α] [StandardBorelSpace α] [Nonempty α]
    {μ : Measure Ω} [IsProbabilityMeasure μ]
    (X : ℕ → Ω → α) (hX_meas : ∀ i, Measurable (X i))
    (hX_exch : Exchangeable μ X) :
    ConditionallyIID μ X :=
  deFinetti X hX_meas hX_exch

Project Structure

Exchangeability/
├── Core.lean                    # Exchangeability definitions, π-systems
├── Contractability.lean         # Exchangeable → Contractable
├── ConditionallyIID.lean        # Conditionally i.i.d. sequences
├── Probability/                 # Probability infrastructure
│   ├── CondExp.lean            # Conditional expectation
│   ├── CondIndep/              # Conditional independence
│   ├── Martingale/             # Martingale convergence
│   └── ...
├── DeFinetti/                   # Three proofs of de Finetti
│   ├── Theorem.lean            # Public API (exports ViaMartingale)
│   ├── ViaMartingale/          # Martingale proof (13 files)
│   ├── ViaL2/                  # L² proof (12 files)
│   ├── ViaKoopman/             # Ergodic proof (18 files)
│   ├── CommonEnding.lean       # Shared final step
│   └── L2Helpers.lean          # L² contractability lemmas
├── Ergodic/                     # Ergodic theory (for Koopman)
│   ├── KoopmanMeanErgodic.lean
│   ├── InvariantSigma.lean
│   └── ProjectionLemmas.lean
├── Tail/                        # Tail σ-algebra machinery
├── PathSpace/                   # Shift operators, cylinders
└── Util/                        # Helper lemmas

Documentation

Blueprint: cameronfreer.github.io/exchangeability/blueprint - Interactive dependency graph and proof status
Status: STATUS.md - Current project status
History: DEVELOPMENT_CHRONOLOGY.md - Project development history

Main Results

Main API

deFinetti — Exchangeable → Conditionally i.i.d. (uses martingale proof)
conditionallyIID_of_contractable — Contractable → Conditionally i.i.d. (martingale/default)
conditionallyIID_of_contractable_viaL2 — L² proof variant
conditionallyIID_of_contractable_viaKoopman — Koopman proof variant

Core Theory

exchangeable_iff_fullyExchangeable — Finite and infinite exchangeability are equivalent
measure_eq_of_fin_marginals_eq — Measures determined by finite marginals

de Finetti's Theorem (Three-way Equivalence)

contractable_of_exchangeable — Exchangeability implies contractability
exchangeable_of_conditionallyIID — Conditionally i.i.d. implies exchangeability

References

Primary Source

Kallenberg, Olav (2005). Probabilistic Symmetries and Invariance Principles. Probability and Its Applications. Springer-Verlag, New York. https://doi.org/10.1007/0-387-28861-9 [Chapter 1, Theorem 1.1]

Additional Sources

De Finetti, Bruno (1937). "La prévision : ses lois logiques, ses sources subjectives." Annales de l'Institut Henri Poincaré 7 (1): 1–68. [English translation: "Foresight: Its Logical Laws, Its Subjective Sources" (1964) in Studies in Subjective Probability, H. E. Kyburg and H. E. Smokler, eds.]
Aldous, David J. (1985). "Exchangeability and related topics." In École d'Été de Probabilités de Saint-Flour XIII—1983, Lecture Notes in Mathematics 1117, pp. 1–198. Springer-Verlag, Berlin. https://doi.org/10.1007/BFb0099421
Ryll-Nardzewski, Czesław (1957). "On stationary sequences of random variables and the de Finetti's equivalence." Colloquium Mathematicum 4 (2): 149–156. https://doi.org/10.4064/cm-4-2-149-156

Hewitt, Edwin and Savage, Leonard J. (1955). "Symmetric measures on Cartesian products." Transactions of the American Mathematical Society 80 (2): 470–501. https://doi.org/10.1090/S0002-9947-1955-0076206-8
Diaconis, Persi and Freedman, David (1980). "Finite exchangeable sequences." The Annals of Probability 8 (4): 745–764. https://doi.org/10.1214/aop/1176994663

License

Apache 2.0

Acknowledgments

This formalization was developed with assistance from:

Claude (Anthropic) - Sonnet 4, Sonnet 4.5, Opus 4.5
GPT (OpenAI) - GPT-5.*-Codex, GPT-5.* Pro

Built with Lean 4 and Mathlib.

exchangeability0.1.0