No results found

Project

Structure in Prime Gaps - Formalized

STRUCTURE IN PRIME GAPS - FORMALIZED

prepared for: https://leanprover.zulipchat.com/

prepared by: KAJANI KAUNDA

Let us lean together! 

import Mathlib

set_option linter.unusedTactic false 
set_option linter.unusedVariables false 

-- ------------------------------------------------------
-- define the cayley table - infinitely defined
-- ------------------------------------------------------

def primes_set := { n | Nat.Prime n }

instance : Infinite primes_set := Nat.infinite_setOf_prime.to_subtype
instance : DecidablePred (fun n => n ∈ primes_set) := 
fun n => Nat.decidablePrime n

def primes (n : ℕ) : ℕ := if (n = 0) then 0 else Nat.Subtype.ofNat primes_set (n - 1)

lemma primes_zero : primes 0 = 0 := rfl

def primes_inv_exists (n : ℕ) (n_prime : Nat.Prime n) : ∃ i, primes i = n :=
by
  have := Nat.Subtype.ofNat_surjective (s := primes_set)
  obtain ⟨a, ha⟩ := this ⟨n, n_prime⟩
  use a + 1
  simp [primes, ha]

def primes_inv (n : ℕ) (n_prime : Nat.Prime n) : ℕ := Nat.find (primes_inv_exists n n_prime)
def primes_inv_def (n : ℕ) (n_prime : Nat.Prime n) : primes (primes_inv n n_prime) = n :=
Nat.find_spec (primes_inv_exists n n_prime)

lemma primes_inv_pos (n : ℕ) (n_prime : Nat.Prime n) : 0 < primes_inv n n_prime :=
by
  rw [zero_lt_iff]
  intro h
  replace h := congrArg primes h
  rw [primes_inv_def, primes_zero] at h
  exact n_prime.ne_zero h

lemma primes_prime {n : ℕ} (hn : n > 0) : Nat.Prime (primes n) :=
by
  unfold primes
  rw [if_neg hn.ne']
  exact Subtype.mem _

def cayley_table (row col : ℕ) : ℤ := primes col - primes row

Structure in Prime Gaps - Formalized

By Kajani Kaunda.

Structure in Prime Gaps

This project formalizes a result from the article Structure in Prime Gaps using Lean 4, the latest version of the LEAN proof assistant. By utilizing Lean 4's robust proof-checking mechanisms, we ensure the correctness and rigor of the findings related to the existence of infinitely many structured gaps between prime numbers.

This formalization contributes to the growing body of work aimed at formalizing mathematical proofs.

The paper Structure in Prime Gaps presents two key results:

  1. Theorem 1: For every prime pα, there exists infinitely many pairs of primes, (pn, pn+m), such that (pn+m − pn) = pα − 3, where n, α ≥ 3, m ≥ 1, and pn is the nth prime.
  1. Theorem 2: There exist infinitely many pairs of primes with a gap of 2.

This repository contains the formalization of Theorem 1 in Lean 4. Theorem 2, which asserts the existence of infinitely many pairs of primes with a gap of 2, follows directly as a corollary of Theorem 1 when pα is set to 5.

A brief visual overview of the results presented in the article Structure in Prime Gaps

The following partial Cayley table T represents gaps between primes in which the results we are formalizing are self-evident.

Consider Table 1, it is not immediately apparent if any useful pattern can be discerned from it. However, with the highlights in Table 2, a compelling pattern emerges, one that leads directly to Theorem 1 from which Theorem 2 is implied as seen in Table 3.

  • Each pattern is defined and identified by the 4-tuple β = (A, B, L, E) formed from the elements in the vertices of a sub-array Ti of T. In Table 2, the first 4-tuple β = (A, B, L, E) for prime 23 is β = (20, 28, 12, 20).

  • Every sub-array TTi, defines two pairs of primes. In Table 2, the First pair is (3, pα) or (3, 23) and the Second pair is (((B + 3) + 0 - E), (B + 3)) or (11, 31). We can denote the integers 11 and 31 in the Second pair using the variables Qi and Ri respectively.

  • The First pair remains constant for all patterns related to any prime pα ≥ 5. Subsequent Second pairs are unique for each sub-array TTi of T.

  • L is always congruent to 0 mod 6.

Legend for Tables:

  • Table 1: Represents the Cayley Table T of the Commutative Partial Groupoid structure (J, +) without immediately discernible patterns highlighted.

  • Table 2: Highlights patterns where the 4-tuple β = (A, B, L, E) defines each pattern, with specific examples provided. The "Pattern" here is more elaborately defined in the sense that it consists of integers other than just Qi and Ri.

  • Table 3: Demonstrates the implication of results derived from the patterns observed in Table 2.

  • Remark: We note that the Cayley Table T is a partial representation of an otherwise infinite structure.

Table 1

Table Legend

Table 2

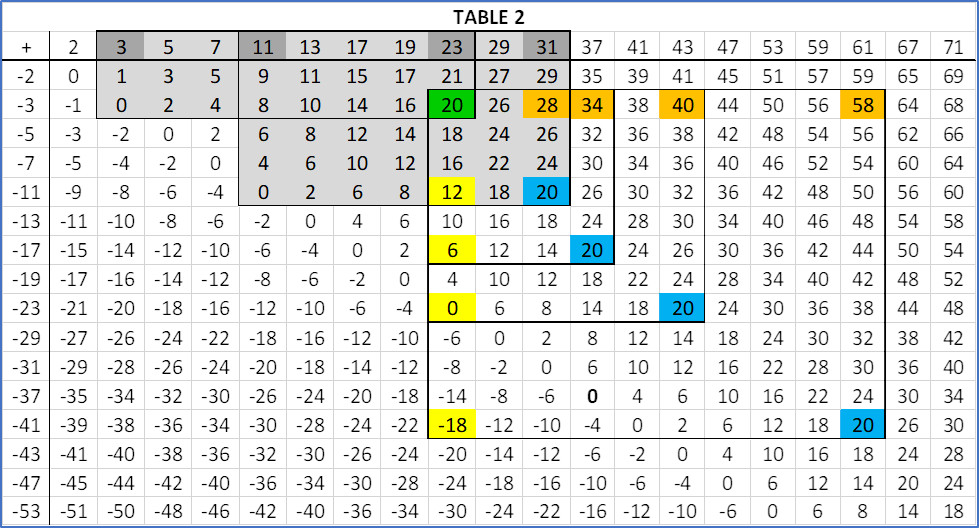
Table 3

Conclusion

By formalizing these results, we hope to contribute to the body of knowledge in mathematics as well as help establish the use of proof assistants like LEAN in academia, research and industry in general.

Implication for the Twin Prime Conjecture

The formalization in Lean 4 establishes that for any fixed prime P' > 3, the subtype

{b : Beta // b.P = P'}

is infinite. This means that for every such prime P', there are infinitely many distinct values of

b : Beta

with fixed P = P', and each such b encodes a structured 4-tuple (A, B, L, E) satisfying

(B + 3) - ((B + 3) - E) = (A + 3) - 3 = P' - 3.

In particular, when we set P' = 5, the structured difference becomes 2, and the above expression reduces to:

E = 2

This gives rise to infinitely many prime pairs of the form:

(B + 1, B + 3)

which is just (p, p + 2)—the standard twin prime form.

Therefore:

The formalization of Theorem 1 in Lean 4 directly implies the twin prime conjecture as a corollary by specializing to the case P' = 5.

This allows us to assert that the present work also constitutes a formalization, within Lean 4, of the Twin Prime Conjecture.

Source References

Useful Links